大数据下的逻辑回归训练模型方法论-难乎？

在数据膨胀的当今社会里，海量数据中蕴含价值日渐凸显出来。如何有效的挖掘海量数据中的有效信息已经成为各个领域面临的共同问题。以互联网企业为代表的科技公司依据自身的实际需求，开始大量的应用机器学习、数据挖掘以及人工智能等算法获取海量数据中蕴含的信息，并且已经取得了很好的效果。

当今社会已经从过去的信息匮乏，转变为信息泛滥的时代。由于网络以及相关应用的不断普及，网络数据逐渐呈现着”海量，高维”的趋势，如何利用已有的机器学习或者数据挖掘的算法，获取有效信息，已经成为学术界以及工业所共同关注的重点。国内大数据技术服务商百分点公司已将机器学习的相关技术应用到大数据分析中，在百分点合作的某一团购网站，我们选取了10个基于商品和用户的特征属性，结合机器学习中的分类算法，构建了一个基于用户推荐的分类器。在实际应用过程中，该团购网站点击率平均提升19%，下单率提升42%，直接下单率提升了近一倍，从而达到了提高推荐效果的目的。

在本篇文章中将以机器学习的经典算法逻辑回归模型作为预测模型，结合目前百分点为团购网站开发的分类模型作为具体实例，具体讲解一下如何在”海量、高维”数据中有效的训练模型。

机器学习算法中的逻辑回归模型(Logic Regression, LR)，以下简称为LR模型，是一个被广泛应用在实际场景中的算法。在本篇文章主要考虑的对象是基于二元分类逻辑回归预测模型，即分类器识别的类标号为。假设训练集数据为，其中，，可以将训练集看成是一个的矩阵，由于在本篇文章中主要针对的是高维的海量数据，但由于哑元变量的存在，数据中存在着大量的0/1值，因此可以将训练集的整体看成是一个高维的稀疏矩阵。

在介绍如何训练模型之前，首先简单的介绍一下逻辑回归模型。逻辑回归模型是一种基于判别式的方法，它假定类的实例是线性可分的，通过直接估计判别式的参数，获得最终的预测模型。逻辑回归模型并不是对类条件密度

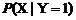
建模，而是对类条件比率进行建模。假定类条件对数似然比是线性的：

使用贝叶斯公式，我们有：

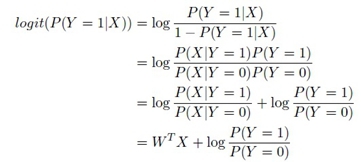
令表示为，因此我们可以得到逻辑回归模型：

作为的估计。

训练逻辑回归模型

当我们确定使用LR模型并且选定了初始特征集，那么我们的下一步就是如何获取最佳的评估参数，使得训练得到的LR模型可以获得最佳的分类效果。这个过程也可以看做是一个搜索的过程，即在一个LR模型的解空间内，如何查找一个与我们设计的LR模型最为匹配的解。为了达到能够获取对应的最佳LR模型，我们需要设计一种搜索策略，考虑按照什么样的准则去选择最优的模型。

如何选择最佳的LR模型，直观的想法就是通过预测模型的结果与真实值的匹配程度评价预测模型的好坏。在机器学习领域中，使用损失函数(loss function)或者代价函数(cost function)来计算预测结果与真实值得匹配程度。损失函数是一个非负实值函数，根据不同的需求，可以设计不同的损失函数。在本篇文章中将作为损失函数，其中

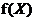
是预测模型f基于测试实例X的预测值，Y是测试实例x的真实类标号的值。

在机器学习中常用的损失函数包括以下几种：

0-1损失函数:

平方损失函数:

绝对损失函数:

对数损失函数或对数似然损失函数:

由于模型的输入和输出（X,Y）是随机变量，遵循联合分布P（X,Y），所以损失函数的期望是：

上面的期望公式表示的是理论预测模型

关于联合分布P（X,Y）在平均意义下的损失，称为风险函数(risk function)或期望损失(expected loss)。损失函数与风险函数实际上都是为了测量预测模型的分类能力，只是前者是从微观层次上考虑，而后者是从宏观上(平均意义上)考虑。因此我们可以获得关于训练数据集的平均损失，称为经验风险(empiricalrisk)或经验损失(empirical loss),记作:

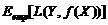
其中

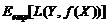
是预测模型关于联合分布的期望损失，而

则是模型关于训练样本的平均损失。根据统计学中的大数定理，当样本容量很大的时候，可以将经验损失作为期望损失。但是在训练模型的过程中，由于数据中存在着噪音数据或者数据偏移的问题，导致了训练模型的泛化性非常差，也就是机器学习中著名的过度拟合的问题。为了解决这个问题，需要规则化处理，人为增加约束条件，在经验风险函数上添加上表示模型复杂度的正则化项(regularizer)或惩罚项(penalty term)，这种经验风险函数被称作结构风险最小化(Structural Risk Minimization, SRM)，可以使用下面的公式表示：

其中

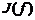
用来惩罚模型的复杂度，模型F越复杂，复杂度

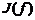
越大，是系数，用以权衡经验风险和模型的复杂度。

在机器学习中，总结起来共有三类方法用来设计相关的经验风险函数：

当设计的模型很简单，并且数据量也很大的时候，给定一组参数以后，可以使用最大似然评估方法(Maximum Likelihood Estimation, MLE)训练得到相关的模型参数；

当设计的模型很复杂，存在着隐含变量。这样的情况可以使用EM算法评估模型的参数。一般分为两个步骤，首先给定参数，对于隐含变量做期望，算出包括隐变量的似然函数；第二步，使用MLE方法，评估参数值，更新对应的参数值；

当模型并不是很复杂，但是数据非常少的时候，并且具有一定的先验知识的时候，可以使用贝叶斯统计方法评估模型的参数，也就是所谓的最大后验概率(Maximum A Posteriori，MAP)。首先基于先验知识，给定待估参数一个先验统计分布，然后根据贝叶斯公式，推算出参数的后验分布(posterior probability)，最后最大化这个后验概率，获得对应的参数值。

由于本篇文章针对的是“高维、海量”的训练数据，并且使用了相对简单的LR模型作为预测模型，因此我们在训练模型的过程中使用了MLE方法，设计相关的经验风险参数;其次由于本身的训练数据充足，因此在经验函数中并没有添加对应的基于模型复杂的惩罚项(正则化)，在我们模型中其具体的风险函数如下所示：

下面的问题就转变为一个无约束的最优化的问题。在基于海量数据训练模型的时候，需要考虑的是如何高效的训练模型。在实际的开发过程中，个人认为可以从两个方面提高训练模型的效率。首先是对于数据在内存的存储结构进行优化，尤其是针对“高维、稀疏”矩阵的时候，在本次实验中我们应用了R中的Matrix包中的稀疏矩阵格式，大幅度提高了算法计算效率。其次需要选择相关的迭代算法，加快经验风险函数的收敛速度。在这里介绍几种常用的迭代算法:

牛顿迭代算法中的牛顿-拉斐森迭代算法，该算法需要计算海森矩阵，因此算法需要花费大量的时间，迭代时间较长。

拟牛顿迭代算法，使用近似算法，计算海森矩阵，从而降低算法每次迭代的时间，提高算法运行的效率。在拟牛顿算法中较为经典的算法有两种：BFGS算法和L-BFGS算法。BFGS算法是利用原有的所有历史计算结果，近似计算海森矩阵，虽然提高了整个算法的效率，但是由于需要保存大量历史结果，因此该算法受到内存的大小的局限，限制了算法的应用范围；而L-BFGS则是正是针对BFGS消耗内存较大的特点，只保存有限的计算结果，大大降低了算法对于内存的依赖。

在实际应用中选择何种迭代算法，需要根据实际需求以及数据本身的特点进行选择，在本次试验我们选取了牛顿-拉斐森迭代算法以及L-BFGS算法作为LR模型的迭代算法。

属性选择

当学习算法迭代完成之后，我们可以获对应各个属性的权重。接下来的任务我们需要对现有属性与响应变量之间的显著性进行检验，针对已有的训练模型对应的属性集进行验证，删除显著性不符合阈值的特征。由于在构建风险函数的时候，使用了MLE方法，因此可以使用Wald Test对于计算得到的参数，进行显著性验证。在使用Wald Test之前，要确保期望值与评估值之间的差值符合正态分布。Wald统计变量的一般形式：

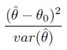
其中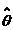表示评估值，表示期望值，表示评估值方差。在本次试验中我们将原假设设定为，即表示现有的属性与响应变量无相关性，因此本实验的Wald统计值可以表示为：

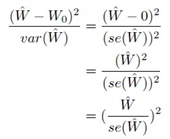
其中是实际估计的参数值，是的标准方差。由于Wald统计值对应卡方分布，因此可以利用卡方分布计算P值，如果P值大于指定的阈值，那么可以认为原假设成立，即该属性与响应变量是显著不相关，删除该变量，否则保存该变量。在实际的训练过程中，每次验证属性显著性的时候，只挑选P值最大与人为设定的阈值进行比较；如果选择的P值不大于阈值，那么模型训练完毕；否则删除选择的P值对应的属性，更新预测模型。重新学习更新后的预测模型，推测对应的权重值，然后再次对各个属性进行Wald Test验证。重复上面的过程，直到没有任何变量的Wald Test对应的P值都不大于人为设定的阈值为止。到此整个模型的训练过程结束。