大数据时代的“因果关系”思辨:相关性和因果性
迈尔舍恩伯格在《大数据时代》里说,“要相关,不要因果”,在大数据时代,有相关,就够了。而周涛则在《为数据而生》一书中说,放弃对因果关系的追寻,就是人类的自我堕落,相关性分析是寻找因果关系的利器。想不想听听第三方的观点?
相关性和因果性之间的联系,从统计学教材到大数据著作,都有着广泛的探讨,甚至争议不断。迈尔舍恩伯格在《大数据时代》里说,“要相关,不要因果”,在大数据时代,有相关,就够了。而周涛则在《为数据而生》一书中说,放弃对因果关系的追寻,就是人类的自我堕落,相关性分析是寻找因果关系的利器。想不想听听第三方的观点?下面文字为BuzzFeed首席数据科学家Adam Kelleher观点的部分编译,感兴趣的读者,请阅读原文。
我们知道,相关关系和因果关系,在人们的工作和生活中,都扮演着极其重要的角色,它们单独或共同影响着我们的行为去向。比如说,经过千百年来的观察,人们发现,“燕子低飞”和“即将下雨”存在相关性,因此,一旦看到“燕子低飞”,人们就知道“天将下雨”,该收衣服了。
至于因果关系,对我们的影响,就更加明显了。一方面,做某个事情前,我们总习惯“给我个理由先”。事后,也爱给自己的行为“结果”,找个“原因”。比如说,“因为我要早晨去上班,所以我必须6点钟起床”。倘若上班迟到了,给老板解释,“因为闹钟没有响,所以我没能准时起床”。千百年来,因果关系,已经深深地写入了人们的思维基因里。
既然相关性和因果性如此重要,二者之间有什么关系呢?在学校里的统计课程中,我们都不断被老师告知,“相关性并不意味着因果性”。那么,相关性意味着什么?有没有一个更好的解释模型,来帮助我们理解这个纷杂的世界呢?为了搞清楚这些问题,我们首先要了解,什么是因果关系?
何谓因果关系
现在因果关系有着非常明确的定义,通常来说,原因是指引起一定现象的现象,结果是指由于原因的作用,随之串联而引起的现象。因果联系的特征就是,原因在先,结果在后,前者的出现,导致后者。但千百年来,有关因果关系的认知,却争议不断。比如说,18世纪英国著名哲学家休谟,压根就不承认有什么因果关系,他认为,所谓的因果关系,只不过是思想中的习惯性联想罢了。
下面我们就用一个例子,来说明常规意义上的因果关系。假设你每天都要到单位上班。显然,如果交通堵塞,会导致你上班迟到。此外,如果家里的闹钟不响(因此你没能准时起床),也会导致你上班迟到。于是,我们就用一个如图1所示的关系图,来描述这这三者(闹钟、交通和迟到)之间的关系。
图1: 基本的因果关系图
图1仅仅列出了两个最常见的上班迟到原因。实际上,迟到的原因可能还包括,车在路上抛锚了,给孩子们做早餐耽搁了,早起看新闻分心了等等,诸如此类。图1不可能把所有的这些小因素都包括在内。
为了抓住主要矛盾,认知的模型必须精简,如图1所示的模型,只能包括在那些最常见的影响我们上班迟到的因素。那些被我们忽略掉的大量的小因素,可以将其视为“噪音”,将其过滤掉。事实上,我们还可以进一步构建一个更全面的“因果关系”的模型图。比如说,我们继续追寻,交通阻塞的原因是什么?闹钟不响的原因是什么?
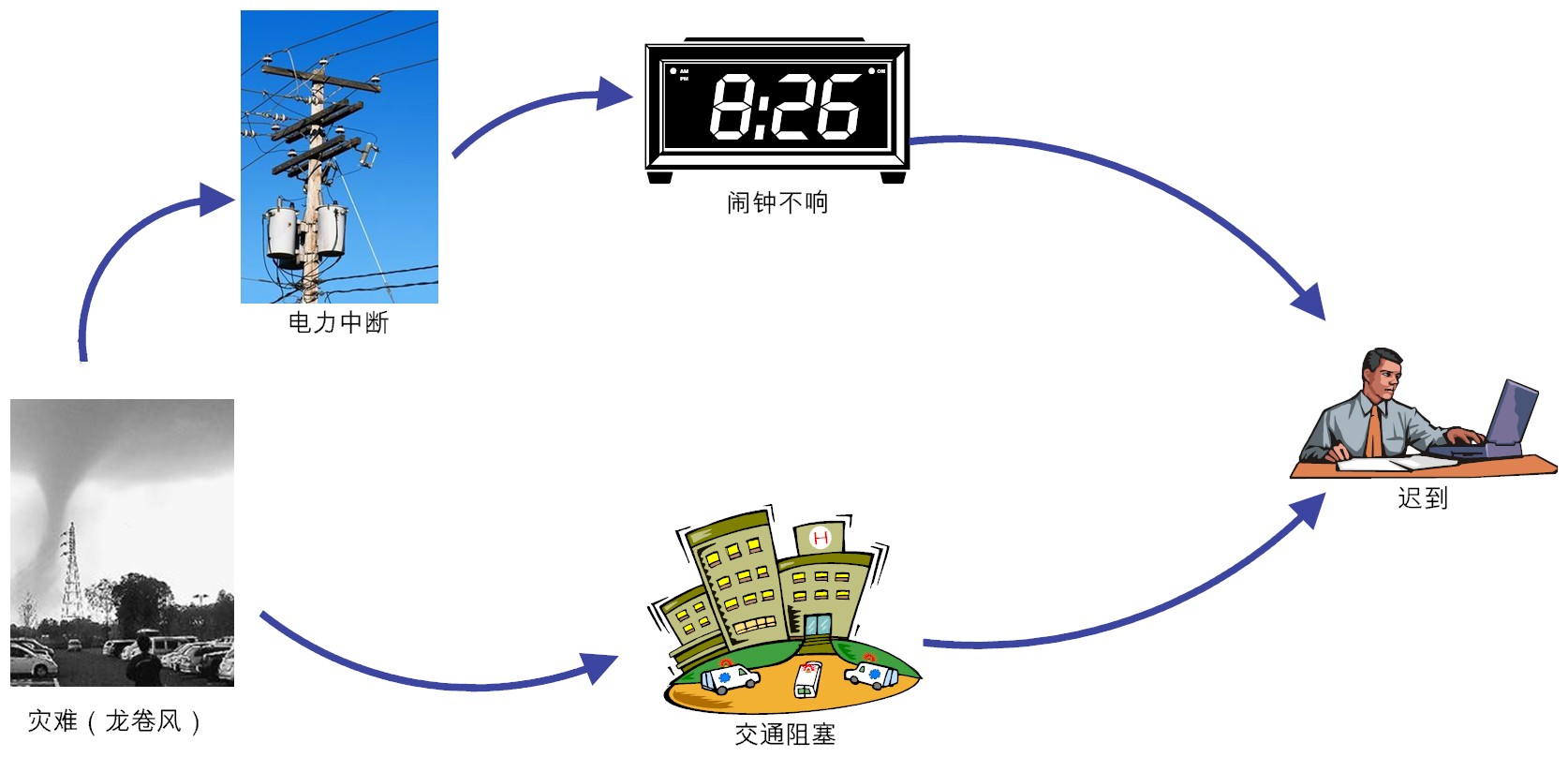
倘若有一场意外灾难(如龙卷风),它导致电力中断,从而闹钟不响了(假设闹钟是插电式的)。意外灾难同样也导致了交通堵塞。于是我们重新更新图1,给出了闹钟失效和交通堵塞的原因,如图2所示。
图2:一个更为完整的世界
如果时间轴线足够长,我们可以收集到大数据集合,然后分析发现,在你家的闹钟不响时,交通也发生阻塞了,很显然,这两个原本“风马牛不相及”的事物,存在相关性。但我们也清楚地知道,闹钟是否响起,和是否有交通阻塞,它们之间是没有因果关系的。这就是“相关性并不意味着因果性”的本质。
更明确点来说,相关性是统计上的概念,数据多了,A发生时B发生的概率,足够显著,那么A和B就是相关的。而因果性是逻辑上的概念,A发生导致B发生。类似的还有,例如,看见闪电(A)和听见雷声(B)是高度相关的,但它们二者相互之间并没有因果关系。
正如前文所言,相关性分析,不是杀死因果关系的凶手,恰恰相反,它是寻找因果关系的利器。相关性的背后,一定有导致A和B发生的共同原因在起作用。这些背后的原因,可能不是直接原因,它可能处于“因果关系图”的“上游”某处。例如,自然灾难就是“闹钟不响”和“交通阻塞”的背后共因。雷雨天气是“打雷”和“闪电”背后的共因
那么,现在问题来了。
如果那些隐藏于相关性背后的共同原因,能找到则罢,但我们又没有“天眼”,不能次次都看透相关性背后的玄机,怎么办?
不用太担心,下面我们看看,我们所依赖的科学,是如何工作的,了解之后,你就会对这个问题更加坦然。
科学是如何工作的?
为了避免进入科技哲学的讨论范畴,我们仅仅根据一些基本原则,对一些观察到事实,进行就事论事的讨论。
现在,假设我们认识的世界,就是根据图1所示来运转的。现在,我们想验证这个假设。在一定程度上,图1所示的世界是“足够好”的,因为“闹钟不响”是能作为“迟到”的原因的,同样,“交通堵塞”也可以解释“迟到”。
因为灾难性事件是非常罕见的。所以,一开始,我们很难发现“闹钟不响”和“交通堵塞”二者之间,存在什么相关性。但随着时间的推移,时间轴线越来越长,在时间域内,越来越多的灾难数据可以被采集到。于是,“闹钟不响”和“交通堵塞”同时出现的情况,愈发频繁,并达到了统计上的显著性。那么,如果我们还用图1来解释整个世界,就显得有点摇摇欲坠了。
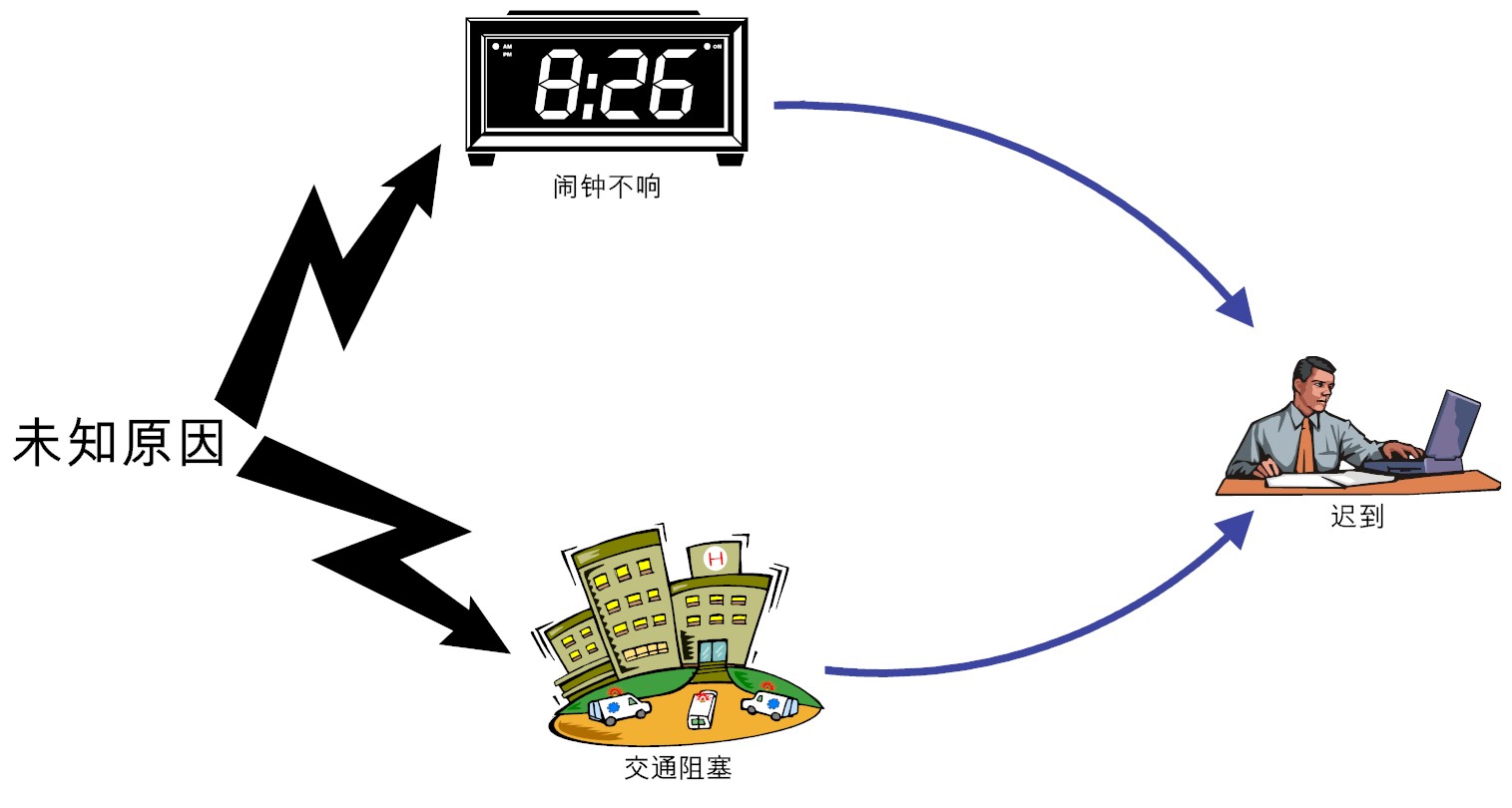
于是,就需要更新我们的认知模型,即用一个双向端箭头,把两个相关的事件连接起来,如图3所示。图中双头箭头是表明,有某些不常见的原因,驱动着的“闹钟不响”和“交通堵塞”这两个事件相关。
图3:一个未观察到的原因
自然,我们很希望这个背后的原因范围,能缩小到图2所示那么精确。但现实是残酷的,很多时候,我们所认知的世界是懵懂的。但是,即使我们没有得到一个如图2所示的精确认知,即使丢失了一些链接和变量,在很多时候,这样的世界已经“足够好”了。
但科学的进步,就是对“足够好”的不满足(Good enough for Science is not good enough)。
在物理学领域,这种类型的科学进步,是有例可循的。比如说,牛顿的万有引力理论,就是一个“足够好”的解释世界的图谱。因为它既可以解释大部分星辰的运转,也足以让人类登上月球。
但是,牛顿定律对“水星进动”(Precession of Mercury)就解释得“不够好”(因为水星近日点进动值与观测值存在分歧)。对于精确GPS系统而言,牛顿定律也是不够用的(因为高精度的GPS测量,除了要考虑GPS系统本身的精度,还应该考虑与地球整体运动有关的相对论效应)。后来,爱因斯坦并没有满足于牛顿“足够好”的知识图谱,于1916年发表了著名的广义相对论,提供了一个更为完整的认知图,能更好的解释这个世界。于是,“水星进动”得以更好的解释,GPS系统可以有更好的精度。
未完的结论
从上面的讨论可知,相关性的确并不意味因果性,但却意味着,在认知图谱的上游,可能蕴含着某些非常见的共因。对这些非常见共因的探寻,能拓展我们的认知图谱。
图2所示的世界,其实是一个比拟。由于在我们的世界里,“灾难(黑天鹅事件)”发生的次数是极少的。所以,我们必须注重收集越来越多的数据,以捕捉这些罕见的结果,一旦我们能够形成对这些罕见结果的可解释性(因果关系),这就会拓展我们的知识边界,提升我们对世界的理解水平。
我们知道,在小样本集合里,很多处于长尾部分的案例,由于发生概率极低,极有可能无法观察到。大数据很重要的一个优势,就是在长尾应用中,发现稀疏而珍贵的价值——对某些罕见结果的可解释性(如某些低频癌症的病因等),这是极其有用的。
欢迎加入本站公开兴趣群
高性能计算群
兴趣范围包括:并行计算,GPU计算,CUDA,MPI,OpenMP等各种流行计算框架,超级计算机,超级计算在气象,军事,航空,汽车设计,科学探索,生物,医药等各个领域里的应用
QQ群:326600878